Volejbal
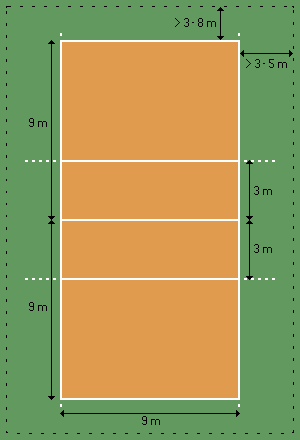 |
| Volejbalové ihrisko |
Volejbal je olympijský šport, v ktorom dve družstvá oddelené vysokou sieťou pomocou svojich rúk, ramien a (zriedka) aj iných častí trupu udierajú do lopty a snažia sa ju premiestniť na opačnú stranu siete.
Volejbal sa zrodil na sklonku 19. storočia v USA. V roku 1895 profesor telesnej výchovy v Holyoku W. G. Morgan rozdelil telocvičňu tenisovou sieťou, ponad ktorú žiaci odbíjali basketbalovú loptu. Rozpracoval prvé základné pravidlá hry a dal jej názov minonette. Prvý raz sa minonette hral pred divákmi v Springfielde v roku 1896. Až neskôr nazvali túto hru volejbalom (odvodené od „to volley the ball“ – odraziť loptu). Prostredníctvom vojakov USA bojujúcich počas prvej svetovej vojny vo Francúzsku sa volejbal dostáva na európsky kontinent v roku 1917. Po úprave pravidiel Medzinárodnou volejbalovou federáciou FIVB sa volejbal zo širokej výkonnostnej základne rýchlo stal vrcholovým športom, ktorý dosahuje veľa významných medzinárodných úspechov.
Volejbal patrí do skupiny odrážacích športových hier s veľkou popularitou na celom svete. Je hrou sieťovou a kolektívnou. Popularita volejbalu vyplýva zo zaujímavého a pestrého obsahu hry, z činností, pri ktorých hráč musí spolupracovať so spoluhráčmi a neprichádza do osobného - priameho kontaktu so súperom. Volejbal je vlastne boj dvoch družstiev, pričom obidve sa snažia realizovať základné úlohy v hre, ktoré rozhodujú o víťazstve. Táto činnosť je charakterizovaná tým, že hráči sa snažia loptu vrátiť do poľa súpera, aby ju súper nemohol spracovať a vrátiť ponad sieť dovoleným počtom odbití. Hráči sa usilujú o dotyk lopty s hracou plochou súpera. Pokiaľ sa to niektorému z tímov podarí, výmena končí a víťazný tím získava bod. Táto činnosť sa realizuje v zápase. V priebehu boja dvoch kolektívov sa strieda útok a obrana. Jedno družstvo útočí a druhé sa bráni, respektíve prechádza do protiútoku. Útočiaci tím sa snaží položiť loptu na súperovu hraciu plochu a obranný tím sa tomu snaží zabrániť. Obranou sa rozumie blokovanie útočiaceho hráča a nasleduje obrana v poli. Hráči sú v poli rozostavení tak, aby zamedzili dotyku lopty s palubovkou. Obrana je postavená tak, aby sa dotyk lopty s palubovkou nikdy nemohol realizovať, avšak najmä v mužskom volejbale končí takmer každá výmena bodom. To robí tento šport zaujímavý nielen z diváckeho hľadiska ale aj taktizovania samotných hráčov. Tieto ucelené časti hry nazývame fázami hry. Obidve základné fázy v hre - útok a obrana - majú rovnaký význam. Každý zápas sa delí na sety. Jednotlivé časti, ktoré začínajú podaním a končia chybou niektorého z družstiev, nazývame rozohrami. Moderný volejbal funguje na špecializácií jednotlivých hráčov. V modernom volejbale hrá volejbal až sedem hráčov. Tím pozostáva z dvoch smečujúcich hráčov, dvoch blokárov, jedného nahrávača a posledný hráč je tzv. univerzál. Siedmy hráč vo volejbale je špeciálny obranný hráč - libero. Pre libera platia špecifické pravidlá. Zavedenie libera do volejbalu malo niekoľko dôvodov. Jedným je posilnenie obrany v poli, iným dôvodom je možnosť aktívneho hrania viac hráčom. V neposlednej rade však post libera ponúkol možnosť hrať vrcholový volejbal aj hráčom s nižším vzrastom.
Matematika
 |
Matematika je väčšinou definovaná ako štúdium zákonitostí štruktúry, zmeny a priestoru. Neformálne ju môžeme tiež nazvať štúdiom „diagramov a čísel“. Z formálneho hľadiska je matematika skúmanie axiomaticky definovaných formálnych štruktúr použitím logiky a matematického označenia. Matematiku možno chápať jednoducho ako rozšírenie hovoreného a písaného jazyka s veľmi presne definovanou slovnou zásobou a gramatikou, s cieľom opisovať a skúmať fyzikálne a konceptuálne vzťahy. Hoci matematika samotná sa väčšinou nepovažuje za prírodnú vedu, špecifické štruktúry skúmané matematikmi majú často pôvod v prírodných vedách, najmä vo fyzike. Matematici sa však zaoberajú aj štruktúrami, ktorých pôvod nie je čisto matematický, napríklad ak poskytujú zovšeobecnenie spájajúce niekoľko odborov alebo zjednodušujú výpočty. Mnohí matematici sa zaoberajú určitými problémami z čisto estetických dôvodov, chápajúc matematiku skôr ako umenie než praktickú, alebo aplikovanú vedu. Niektorí matematici nazývajú matematiku „kráľovnou vied“.
 |
Hlavné odvetvia matematiky vznikli z potreby robiť výpočty pre účely obchodu, merať pozemky a predpovedať astronomické udalosti. Tieto tri potreby približne zodpovedajú rozdeleniu matematiky na štúdium štruktúry, priestoru a zmeny. Štúdium štruktúry začína pojmom čísla. Najskôr boli známe prirodzené a celé čísla a ich aritmetické operácie, ktoré sú zahrnuté v elementárnej algebre. Zložitejšie vlastnosti celých čísel skúma teória čísel. Skúmanie metód na riešenie rovníc viedlo k vzniku abstraktnej algebry, ktorá okrem iného skúma štruktúry ako okruhy a polia, ktoré zovšeobecňujú vlastnosti dobre známych aritmetických operácií na číslach. Vektor je pojem dôležitý vo fyzike. Lineárna algebra, ktorá študuje vektory a ich zovšeobecnenie, vektorové priestory, sa nachádza na priesečníku štúdia štruktúry a priestoru. Štúdium priestoru vychádza z geometrie. Najskôr sa rozvíjala euklidovská geometria a trigonometria dobre známeho trojrozmerného priestoru. Neskôr bola euklidovská geometria zovšeobecnená na neeuklidovské geometrie, ktoré majú dôležitú úlohu v všeobecnej teórii relativity. Niekoľko ťažkých geometrických problémov týkajúcich sa konštrukcií pomocou pravítka a kružidla bolo vyriešených pomocou Galoisovej teórie. Moderné odvetvia diferenciálnej a algebraickej geometrie rozširujú geometriu v nových smeroch. Diferenciálna geometria sa sústredí na pojmy funkcie, derivácie a smeru, kým algebraická geometria definuje geometrické objekty ako množiny riešení polynomiálnych rovníc. Teória grúp skúma pojem symetrie, spája štúdium priestoru a štruktúry. Topológia spája štúdium priestoru a zmeny s dôrazom na koncept kontinuity. Prírodné vedy často skúmajú zmenu merateľných veličín a matematická analýza na to poskytuje užitočné nástroje. Základným pojmom používaným na popísanie zmeny je pojem funkcie. Mnohé problémy sa dajú vyjadriť ako vzťah medzi veličinou a rýchlosťou jej zmeny. Metódy na riešenie takýchto vzťahov skúma odbor diferenciálnych rovníc. Spojité veličiny sú reprezentované reálnymi číslami. Vlastnosti reálnych čísel a funkcií nad reálnymi číslami skúma reálna analýza. Z viacerých príčin sa často hodí pracovať s komplexnými číslami, ktoré študuje komplexná analýza. Funkcionálna analýza sa zaoberá priestormi funkcií, ktoré majú väčšinou nekonečne veľa rozmerov. Toto štúdium poskytuje okrem iného matematický základ kvantovej mechaniky. Teória chaosu vznikla z dôvodu, že mnohé z prírodných javov tvoria dynamické systémy, ktoré majú nepredpovedateľné ale deterministické správanie. Teória množín, matematická logika a teória modelov vznikli s cieľom skúmať základy matematiky. Keď vznikla myšlienka počítačov, matematici zaviedli niekoľko dôležitých teoretických pojmov, ktoré viedli k vzniku odborov ako teória vypočítateľnosti, teória výpočtovej zložitosti, teória informácie a algoritmická teória informácie. Tieto odbory sú dnes časťou teoretickej informatiky. Diskrétna matematika je spoločné meno pre odbory matematiky obzvlášť užitočné v informatike. Dôležitým odborom aplikovanej matematiky je štatistika, ktorá používa teóriu pravdepodobnosti ako nástroj na opis, analýzu a predpoveď javov a používa sa vo všetkých vedách. Numerická analýza skúma metódy na efektívne riešenie rôznych matematických problémov na počítačoch a zaokrúhľovacie chyby, ktoré pri numerickom riešení vznikajú.